[비선형 구조] 트리 Tree

트리 Tree란?
계층적 관계(Hierarchical Relationship), 부모-자식 관계를 표현하는 비선형 자료구조입니다.
트리는 사이클이 없고, 서로 다른 두 노드를 잇는 길이 하나인 그래프의 일종입니다.
컴퓨터의 Directory 구조, 조직도, 족보 등이 트리의 대표적인 예입니다.

 

• 트리 구성요소

1. 노드 Node: 트리를 구성하고 있는 각각의 요소
2. 간선 Edge: 트리를 구성하기 위해 노드와 노드를 연결하는 선, 노드가 N개이면 간선은 N-1개를 가짐
3. 루트 노드 Root Node: 트리 구조에서 최상위에 있는 노드
4. 단말 노드 Terminal Node(외부 노드 External Node, Leaf Node): 자식 노드가 없는 노드
5. 내부 노드 Internal Node(비단말 노드): 하나 이상의 자식이 있는 노드, 단말 노드를 제외한 모든 노드(루트 노드 포함)
6. 서브 트리 Sub Tree: 큰 트리에 속하는 작은 트리
7. 형제 Siblings: 동일한 부모를 가진 지식 노드들
8. 조상 Ancestor: 특정 노드의 위에 위치한 모든 노드
9. 자손 Descendent: 특정 노드의 아래에 위치한 모든 노드
10. 깊이 Depth: 루트 노드에서 어떤 노드에 도달하기 위해 거쳐야하는 간선의 수
11. 레벨 Level: 트리에서 각 층별로 숫자를 매김, 루트의 레벨 = 0
12. 높이 Height: 루트 노드에서 가장 먼 단말 노드까지의 간선의 수, 트리의 최고 레벨

 

---

이진 트리 Binary Tree

루트 노드를 중심으로 두 개의 서브 트리로 나뉘어지고 나뉘어진 그 서브 트리의 모든 서브 트리도 이진 트리인 트리입니다.

이진 트리에서는 공집합도 노드로 인정하기 때문에, 서브 트리가 하나이거나 없는 경우도 이진 트리에 속합니다.

이진 트리의 종류는 포화 이진 트리, 완전 이진 트리, 정 이진 트리가 있습니다.

Binary Tree

• 배열로 구성된 이진 트리의 부모, 자식 노드의 index 값 구하는 방법

루트 노드의 index가 0이 아닌 1에서 시작될 때, i번째 노드에 대해서

1. parent(i) = i/2
2. left_child(i) = 2*i
3. right_child(i) = 2*i + 1

 

• 이진 트리의 순회 방법

1. 전위 순회 Preorder Traversal

루트 노드-> 왼쪽 서브 트리 -> 오른쪽 서브 트리

1 -> 7 -> 2 -> 6 -> 5 -> 11 -> 9 -> 9 -> 5

 

2. 중위 순회 Inorder Traversal

왼쪽 서브 트리 -> 루트 노드 -> 오른쪽 서브 트리

2 -> 7 -> 5 -> 6 -> 11 -> 1 -> 9 -> 5 -> 9

 

3. 후위 순회 Postorder Traversal

왼쪽 서브 트리 -> 오른쪽 서브 트리 -> 루트 노드

2 -> 5 -> 11 -> 6 -> 7 -> 5 -> 9 -> 9 -> 1

 

 

• 포화 이진 트리 Perfect Binary Tree

 

Perfect Binary Tree

모든 레벨이 꽉 찬 이진 트리를 말합니다.

모든 내부 노드들이 2개의 자식 노드를 가지고 있고 모든 단말 노드들의 Depth와 Level이 같은 트리입니다.

포화 이진 트리는 정 이진 트리이면서 완전 이진 트리입니다.

 

 

• 완전 이진 트리 Complete Binary Tree

 

Complete Binary Tree

노드가 위에서 아래로, 왼쪽에서 오른쪽으로 순서대로 차곡차곡 채워진 이진 트리를 말합니다.

즉, 마지막 레벨을 제외한 모든 레벨의 노드가 꽉 찬 트리입니다.

 

 

• 정 이진 트리 Full Binary Tree

 

Full Binary Tree

모든 노드가 0개 혹은 2개의 자식 노드만을 갖는 이진 트리를 말합니다.

 

---

이진 탐색 트리 BST, Binary Search Tree

Binary Search Tree

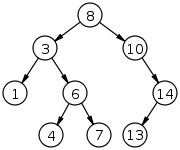
이진 탐색 트리는 이진 트리의 일종으로, 데이터를 저장하는 규칙이 있어 특정 데이터의 위치를 찾을 때 효율적인 탐색이 가능합니다.

연결 리스트로 구현한 이진 탐색 트리의 탐색 연산은 O(log2 n)의 시간복잡도를 가집니다.

정확하게는 트리의 높이만큼의 시간복잡도 O(h)가 소요됩니다.

트리의 높이를 하나씩 더해갈수록 추가할 수 있는 노드의 수가 2배씩 증가하기 때문입니다.

이진 탐색 트리는 삽입 순서에 따라 균형 트리가 될 수도 있고, 편항 트리가 될 수도 있습니다.

 

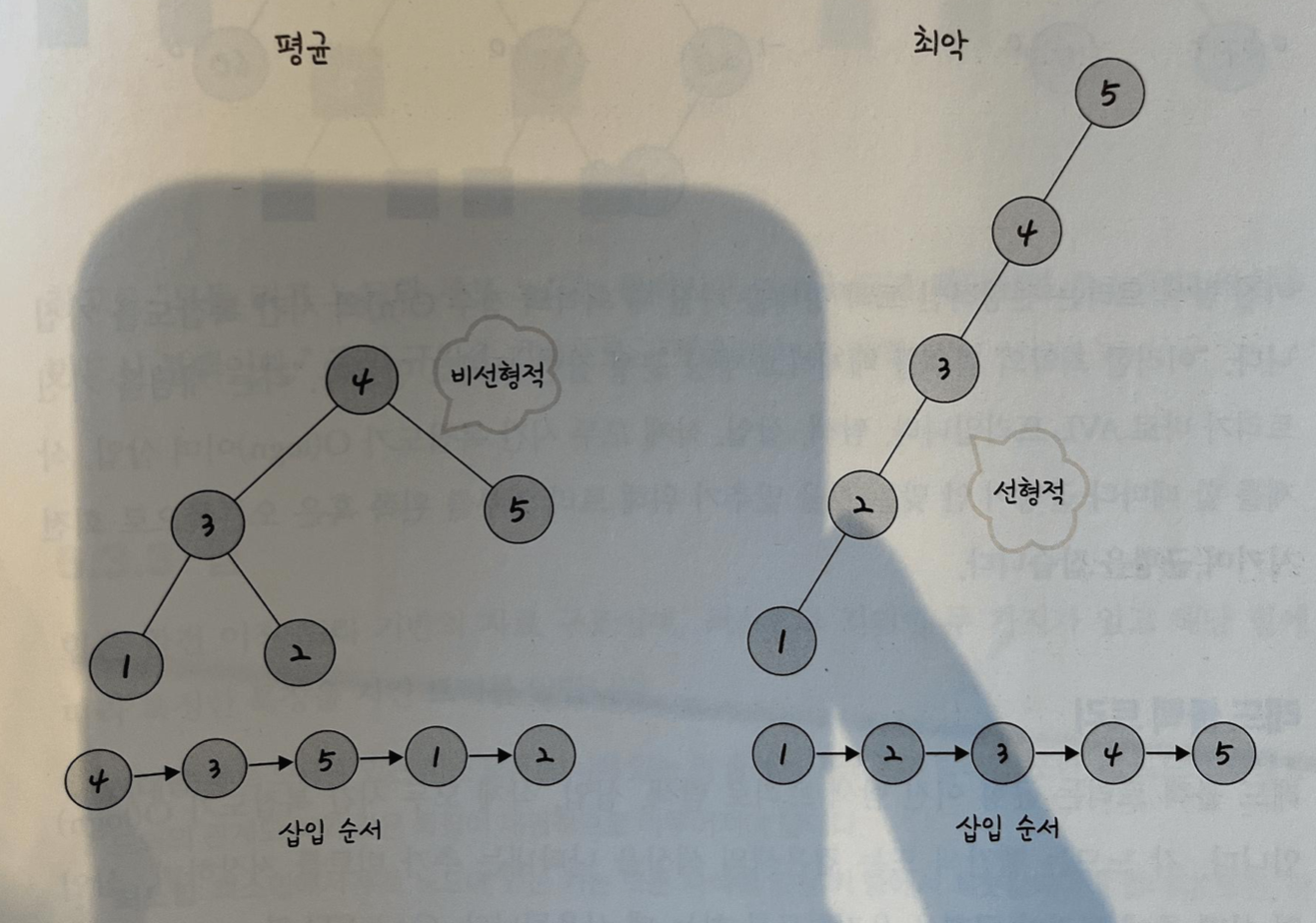
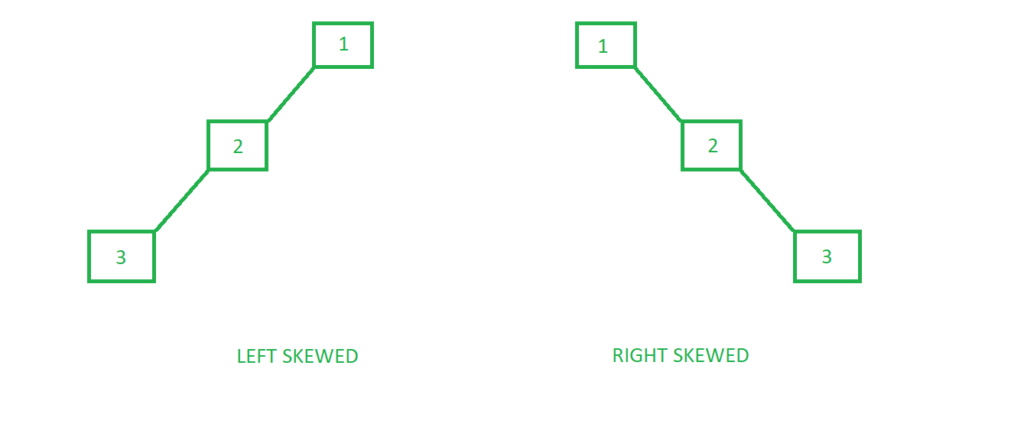
노드가 한 쪽 서브 트리에만 쏠려서 균형이 맞지 않은 편향 트리(Skewed Tree)의 경우, 탐색의 최악의 경우로 노드의 수만큼의 시간복잡도 O(n)이 소요될 수 있습니다.

이 경우 배열보다 많은 메모리를 사용해서 데이터를 저장했지만(포인터를 위한 공간이 필요하기 때문), 특정 값을 찾는 탐색에 필요한 시간복잡도가 같으므로 비효율적입니다.

따라서, 트리의 균형을 잡기 위해 트리의 구조를 재조정하는 Rebalancing 기법을 활용해야 합니다.(AVL Tree와 Red-black Tree가 자가 균형 이진 탐색 트리의 종류입니다.)

 

• 이진 탐색 트리의 데이터 저장 규칙

1. 이진 탐색 트리의 노드에 저장된 키(Key)는 유일합니다.
2. 루트 노드의 키가 왼쪽 서브 트리를 구성하는 어떠한 노드의 키보다 큽니다.
3. 루트 노드의 키가 오른쪽 서브 트리를 구성하는 어떠한 노드의 키보다 작습니다.
4. 왼쪽과 오른쪽 서브 트리도 이진 탐색 트리입니다.

---

AVL Tree, Andelson-Velsky and Landis Tree

이진 탐색 트리가 편향 트리가 되지 않도록 균형을 유지하는 자가 균형 이진 탐색 트리(Self-balancing Binary Search Tree)입니다.

루트 노드의 양쪽 서브 트리의 높이가 최대 1만큼 차이가 나는 특징이 있습니다.

탐색/삽입/삭제 모두 시간복잡도가 O(log n)입니다.

삽입/삭제 시에 균형이 맞지 않으면 트리 일부를 왼쪽이나 오른쪽으로 회전시키는 로직을 통해 균형을 유지합니다.

 

 

Red-black Tree, RBT

Red-black Tree는 자가 균형 이진 탐색 트리(Self-balancing Binary Search Tree)로서, 트리에 n개의 노드가 있을 때 O(log n)의 시간복잡도로 삽입/삭제/검색을 할 수 있습니다.

각 노드에 Red/Black 색깔을 나타내는 추가 비트를 저장해서 삽입/삭제 시에 트리의 균형을 유지하도록 하는데 사용합니다.

특정 노드를 기준으로 왼쪽 서브 트리의 모든 노드의 값은 작거나 같고, 오른쪽 서브 트리의 모든 노드의 값은 크거나 같습니다.

따라서 중위 순회를 하면 오름차순으로 데이터를 탐색할 수 있습니다.

 

루트 노드로부터 단말 노드까지의 모든 경로 중에 최소 거리와 최대 거리의 차이는 항상 2배보다 작으므로 Balanced 상태라고 합니다.

자식 노드가 없는 노드의 child 포인터에는 NIL 값을 저장하고, NIL을 단말 노드로 간주합니다.

Red-black Tree

• Red-black Tree의 조건

1. 각 노드는 Red or Black의 색깔을 갖는다.
2. 루트 노드의 색은 Black이다.
3. 각 단말 노드(NIL)의 색은 Black이다.
4. 색깔이 Red인 노드의 두 자식 노드의 색깔은 모두 Black이다.(Red인 노드는 연달아 나타날 수 없고, Black 노드만이 Red 노드의 부모 노드가 될 수 있음)
5. 어떤 노드로부터 시작되어 그에 속한 하위 단말 노드에 도달하는 모든 경로에는 단말 노드를 제외하면 모두 같은 개수의 Black 노드가 있다.(Black-height가 같음)

* Black-height

특정 노드로부터 단말 노드까지의 경로에 있는 Black 노드의 개수

 

 

• 삽입 Insert

BST 특성을 유지하면서 노드를 삽입하고, 삽입한 노드의 색깔을 Red로 지정합니다.

Red로 지정함으로써 Black-height 변경을 최소화할 수 있습니다.

삽입 결과 RBT 조건에 위배된다면 노드의 색깔을 조정하고, Black-height이 위배되면 rotation을 통해 height을 조정합니다.

이를 통해 Black-height이 같아지고, 최소 경로와 최대 경로의 거리가 2배보다 작게 유지됩니다.

 

 

• 삭제 Delete

BST 특성을 유지하면서 노드를 삭제하며, 삭제할 노드의 자식 노드의 개수에 따라 rotation 방법이 달라집니다.

삭제할 노드가 Black이라면 Black-Height가 감소하므로 Black 노드가 1개 추가될 수 있도록 rotation을 수행하며 색깔을 조정합니다.

삭제할 노드가 Red라면 RBT 조건에 위배되지 않고 유지됩니다.

---

힙 Heap

Max Heap

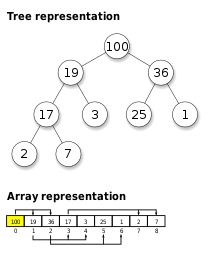
힙은 완전 이진 트리의 구조입니다.

부모 노드의 값이 자식 노드의 값보다 크거나 같으면 최대 힙 Max Heap이고, 부모 노드의 값이 자식 노드의 값보다 작거나 같으면 최소 힙 Min Heap입니다.

Max Heap에서는 루트 노드에 있는 값이 가장 크기 때문에 최댓값을 찾는데 O(1)이 소요되며, Min Heap에서는 루트 노드에 있는 값이 가장 작아서 최솟값을 찾는데 O(1)이 소요됩니다.

힙은 배열을 기반으로 구현하며, 0번 index는 건너 뛰고 1번째 index부터 루트 노드로 시작됩니다.

노드의 고유번호 값과 배열의 index 값을 일치시킴으로써 자식/부모 노드의 index 값을 활용해서 Random Access하기에 용이합니다.

 

• 자식 노드, 부모 노드의 index 값 구하기

1. 왼쪽 자식 노드 = 부모 노드의 index * 2
2. 오른쪽 자식 노드 = 부모 노드의 index * 2 + 1
3. 부모 노드 = 자식 노드의 index // 2

 

• Heapify

삭제/삽입 후에 힙 구조를 유지시키기 위해 Heapify 과정을 거쳐야 합니다.

루트 노드를 삭제한 후에 힙의 맨 마지막 노드를 루트 노드로 대체시키고 자식 노드와의 비교를 통해 제자리를 찾아갑니다.

데이터를 삽입할 때에는 가장 마지막 위치에 저장한 후, 부모 노드와 우선순위를 비교해가며 위치를 바꿔나가면서 제자리를 찾아갑니다.

따라서 삽입/삭제 시에 트리의 높이만큼 비교연산을 진행하기 때문에 시간복잡도는 O(log2 n)입니다.

 

* 힙을 연결 리스트가 아닌 배열로 구현하는 이유

연결 리스트를 기반으로 힙을 구현하면, 새로운 노드를 삽입할 때 마지막 위치에 추가해주기 위해 노드를 탐색해나가는 과정이 소요됩니다.

배열을 기반으로 힙을 구현해야 index 값을 통해 부모와 자식 노드에 쉽게 접근할 수 있기 때문에 배열로 구현하는 것이 효율적입니다.

 

---

우선순위 큐 Priority Queue

데이터가 들어간 순서와 관계없이 우선순위가 가장 높은 데이터가 먼저 나오는 구조로 힙을 기반으로 구현합니다.

 

• 우선순위 큐를 배열/연결 리스트/힙으로 구현한다면?

1. 배열로 구현하는 경우

우선순위가 높은 순서대로 배열의 맨 앞부터 위치시킵니다.

따라서 우선순위가 가장 큰 데이터는 0번 index로 바로 반환할 수 있어 O(1)이 소요됩니다.

하지만 우선순위가 가장 낮은 데이터를 삽입할 때, 삽입할 위치를 찾기 위해 배열의 맨 앞부터 차례대로 비교해야 하므로 O(n)이 소요됩니다.

삽입할 위치를 찾고 그 뒤에 있는 나머지 데이터를 한 칸씩 뒤로 밀어줘야하는 Shift 연산도 필요합니다.

 

2. 연결 리스트로 구현하는 경우

배열과 달리 삽입/삭제 시 Shift 연산은 필요하지 않지만, 여전히 삽입할 위치를 찾기 위해 첫 번째 노드부터 차례대로 우선순위를 비교하는 연산이 소요됩니다.(O(n))

Head에 저장된 우선순위가 가장 높은 데이터를 반환하는데 걸리는 시간은 O(1)이 소요됩니다.

 

3. 힙으로 구현하는 경우

데이터 삽입/삭제 시 힙의 구조를 유지하기 위한 Heapify 연산을 수행합니다.

트리의 높이만큼만 비교 연산이 이뤄지기 때문에 O(log2 n)이 소요되어 배열이나 연결 리스트로 구현했을 때보다 성능이 뛰어납니다.

 

---

출처

• 참고 도서: 면접을 위한 CS 전공지식 노트 - 주홍철 지음

• https://adrianmejia.com/data-structures-for-beginners-trees-binary-search-tree-tutorial/

Tree Data Structures in JavaScript for Beginners

• https://www.geeksforgeeks.org/print-middle-level-perfect-binary-tree-without-finding-height/

Print middle level of perfect binary tree without finding height - GeeksforGeeks

• https://www.geeksforgeeks.org/skewed-binary-tree/

Skewed Binary Tree - GeeksforGeeks

• https://en.wikipedia.org/wiki/Binary_search_tree

Binary search tree - Wikipedia

• https://en.wikipedia.org/wiki/Binary_tree

Binary tree - Wikipedia

• https://ko.wikipedia.org/wiki/힙_(자료_구조)

힙 (자료 구조) - 위키백과, 우리 모두의 백과사전

• https://github.com/JaeYeopHan/Interview_Question_for_Beginner/tree/master/DataStructure#stack-and-queue

GitHub - JaeYeopHan/Interview_Question_for_Beginner: Technical-Interview guidelines written for those who started studying progr

• https://ko.wikipedia.org/wiki/레드-블랙_트리

레드-블랙 트리 - 위키백과, 우리 모두의 백과사전