그래프 Graph란?
간선 Edge과 정점 Vertex으로 이루어진 자료구조이며, 정점 간의 관계를 표현하는 조직도입니다.
정점에는 데이터가 저장되며, 간선을 통해 정점과 정점 사이의 관계를 알 수 있습니다.

- 그래프 용어
- 정점(Vertex, 노드 Node): 데이터가 저장됨
- 간선(Edge, 링크 Link): 정점들을 연결하는 선, 정점과 정점 사이의 관계를 표현
- 인접 정점(Adjacent Vertex): 간선에 의해 연결된 정점(6과 4는 서로 인접 정점임)
- 차수(Degree): 무방향 그래프에서 각 정점에 연결된 Edge의 개수(5의 차수는 3)
- 진출 차수(Out-degree): 방향 그래프에서 각 정점으로부터 나가는 간선의 개수
- 진입 차수(In-degree): 방향 그래프에서 각 정점으로 들어오는 간선의 개수
- 경로 길이(Path Length): 경로에서 연결된 간선의 수
- 사이클(Cycle): 경로의 시작 정점과 종료 정점이 동일한 경우
- 무방향 그래프(Undirected Graph)와 방향 그래프(Directed Graph)

무방향 그래프는 정점을 연결하는 간선에 방향이 없는 그래프를 말하며, 방향 그래프는 간선에 방향이 존재하는 그래프를 말합니다.
- 가중치 그래프(Weight Graph)와 부분 그래프(Sub Graph)

가중치 그래프는 간선에 가중치(비용)가 할당된 그래프를 말합니다.

부분 그래프는 그래프의 일부 정점 및 간선으로 이루어진 그래프를 말합니다.
- 완전 그래프(Complete Graph)와 연결 그래프(Connected Graph)
완전 그래프는 간선을 최대한으로 가진 그래프를 말합니다.
n개의 정점을 갖는 무방향 그래프인 경우 간선의 수는 n(n-1)/2입니다.
n개의 정점을 갖는 방향 그래프인 경우 간선의 수는 n(n-1)입니다.

연결 그래프는 서로 다른 두 정점 사이의 경로가 존재하는 그래프를 말합니다.
모든 정점들에 대해서 임의의 두 정점 사이에 경로가 존재합니다.

- 그래프 구현 방법
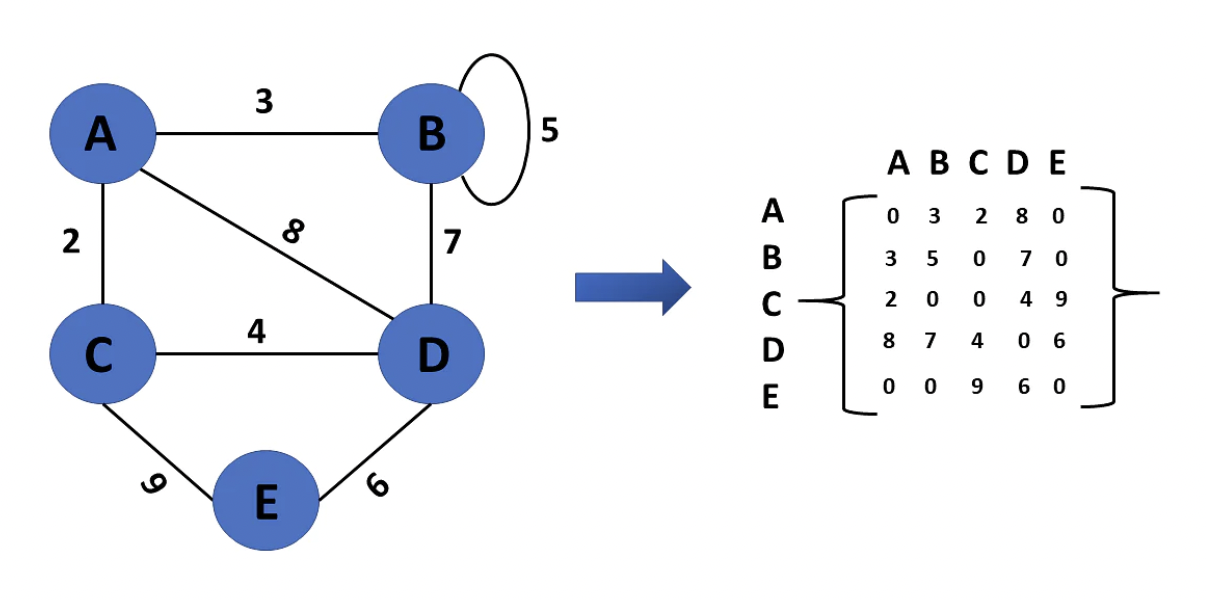
1. 인접 행렬(Adjacent Matrix)
그래프에서 정점이 어느 정점과 연결되어 있는지를 2차원 배열로 나타냅니다.
adj[i][j] = n으로 정점 사이의 연결 관계를 표현합니다.
정점 i와 j 사이에 간선이 없으면 n = 0, 가중치가 없는 그래프에서 간선이 있으면 n = 1, 가중치 그래프에서 간선이 있으면 n = 가중치입니다.
배열을 사용하므로 그래프 구현이 비교적 쉽고, 정점 간 연결 관계를 O(1)로 파악할 수 있다는 장점이 있습니다.
반면, 간선의 개수와 무관하게 V^2의 공간복잡도를 갖으므로 노드의 개수에 비해 간선의 개수가 훨씬 적은 그래프의 경우 비효율적입니다.
초기에 간선 정보를 대입하기 위해 O(V^2) 시간복잡도가 소요된다는 단점이 있습니다.
노드 i에 연결된 노드들을 체크하기 위해서 adj[i][1] ~ adj[i][V]를 모두 탐색하므로 O(V)가 소요됩니다.

무방향 그래프의 경우 대각 성분을 기준으로 대칭인 특성이 있습니다.

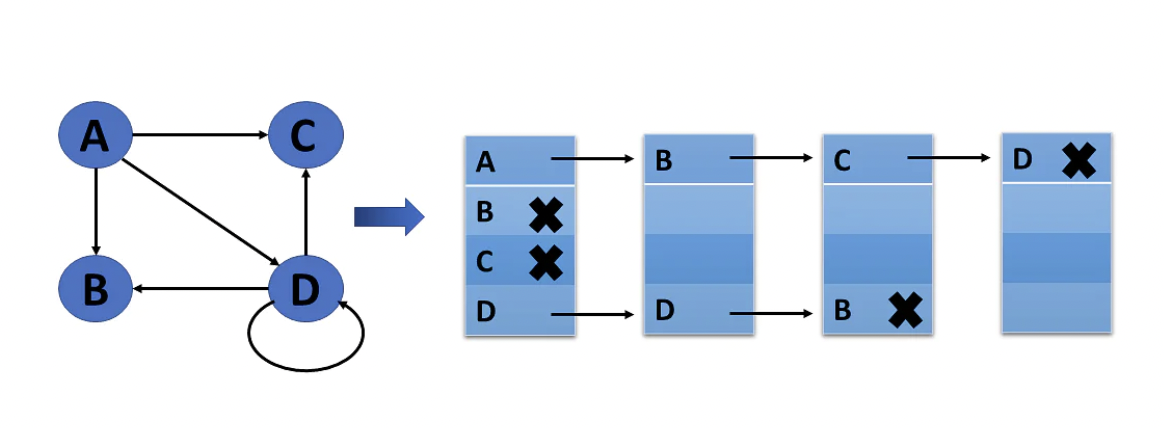
2. 인접 리스트(Adjacent List)
그래프의 한 정점에서 연결되어 있는 정점들을 연결 리스트로 표현하는 방법입니다.
adj[i]에 정점 i와 연결되어 있는 다른 정점들이 연결 리스트로 연결되어 있습니다.
따라서 정점 i와 j가 연결되어 있는지 확인하기 위해서는 adj[i]의 노드들을 하나씩 확인해야 합니다.
구현이 비교적 어려우며, 정점 간 연결 관계를 파악할 때 O(n)의 시간복잡도가 소요된다는 단점이 있습니다.
인접 행렬 방식과 달리, 간선의 개수만큼 노드를 추가되므로 O(V+E)의 공간복잡도가 소요된다는 장점이 있습니다.
그래프 탐색
그래프의 모든 정점을 탐색하는 완전 탐색 알고리즘으로 깊이 우선 탐색과 너비 우선 탐색이 있습니다.
2021.03.18 - [Computer Science/Algorithms] - [완전 탐색]BFS와 DFS
[완전 탐색]BFS와 DFS
Summary BFS와 DFS는 그래프의 모든 정점을 탐색하는(그래프의 순회) 완전 탐색 알고리즘이다. BFS는 Breadth-First Search로 너비 우선 탐색을 의미하고 자료구조는 Queue를 사용한다. DFS는 Depth-First Sea..
hwayomingdlog.tistory.com
- 깊이 우선 탐색(DFS, Depth First Search)
임의의 한 정점에 연결된 간선을 따라 깊이를 우선적으로 탐색해 나가는 방법입니다.
즉, 연결 되어 있는 노드들을 따라 깊숙히 탐색해 나가며, 더이상 연결된 정점이 없으면 바로 전 정점으로 돌아가 연결된 다른 정점을 따라 탐색해 나갑니다.
따라서 방문한 정점으로 되돌아가는 것을 구현하기 위해 스택 Stack 자료구조를 활용하거나, 재귀 함수로 구현합니다.
탐색한 정점들을 스택에 쌓음으로써 직전에 방문한 정점이 스택의 Top에 쌓입니다.
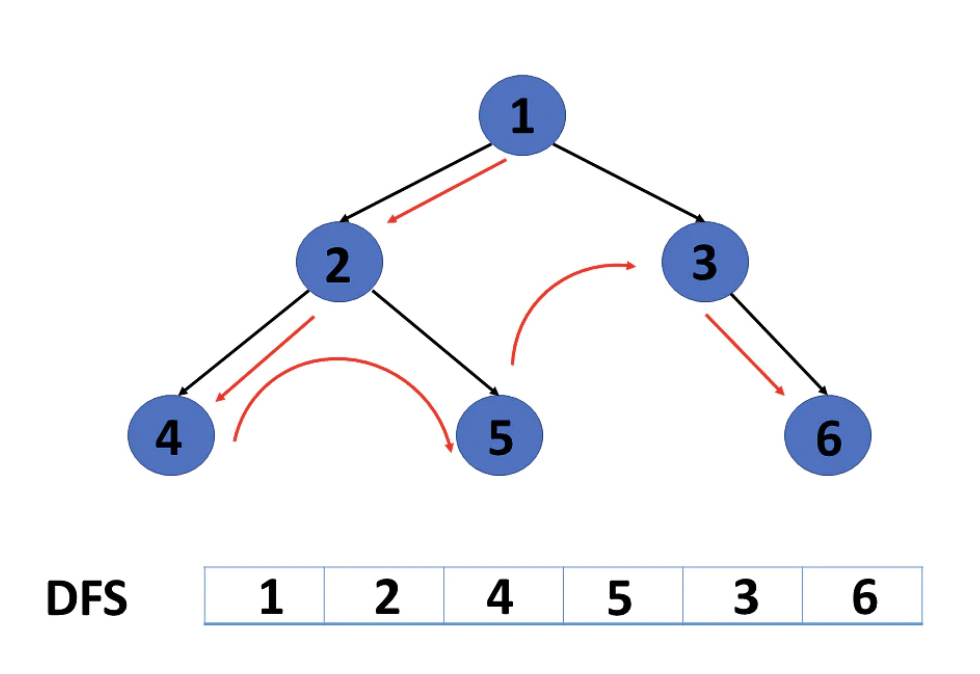
깊이 우선 탐색의 시간복잡도는 O(V+E)가 소요됩니다.
- 너비 우선 탐색(BFS, Breadth First Search)
BFS는 임의의 정점과 간선으로 연결된 인접한 정점들을 먼저 탐색해 나가는 방법입니다.
즉, 너비를 넓혀나가면서 탐색해 나갑니다.
큐 Queue는 BFS 구현을 위해 활용됩니다.방문한 정점과 연결되어 있는 정점들을 큐에 하나씩 담고, 담긴 순서대로 정점들을 방문해 나갑니다.
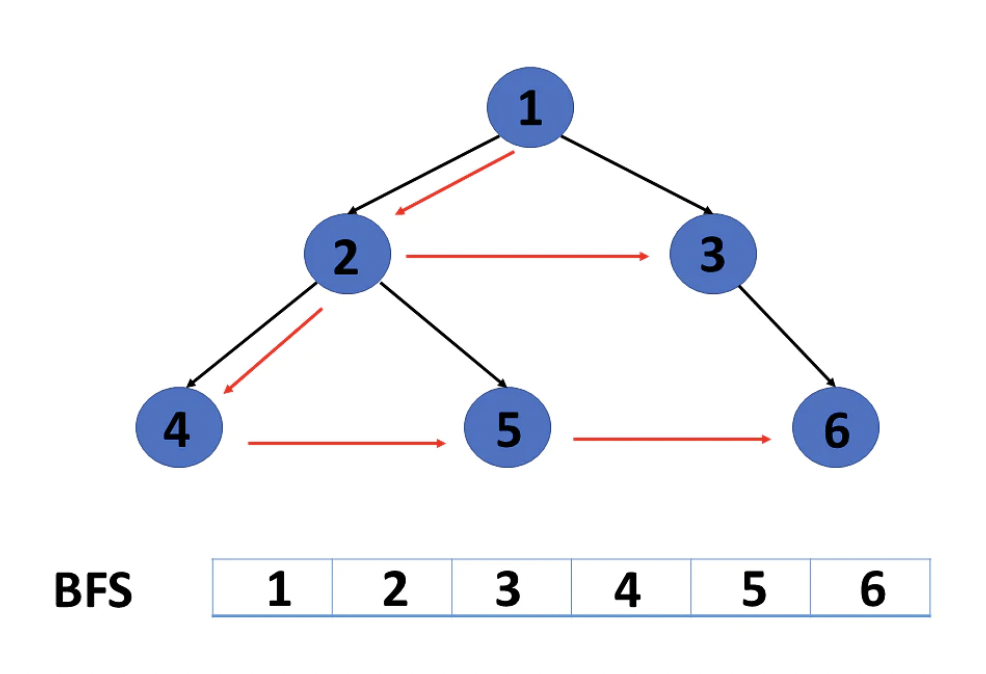
너비 우선 탐색의 시간복잡도는 O(V+E)가 소요됩니다.
신장 트리 Spanning Tree
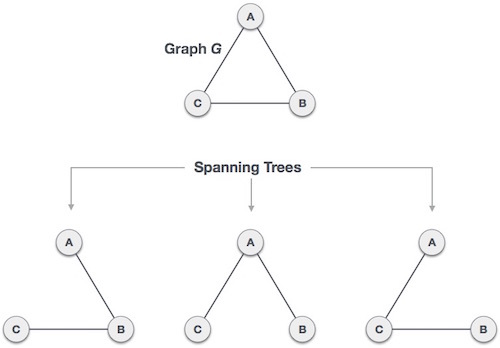
- 신장 트리의 조건
- 연결 그래프의 부분 그래프이며, 모든 정점을 포함합니다.
- 모든 정점에 대해 임의의 두 정점은 서로 연결되어 있어야 합니다.
- 사이클이 없습니다.
- 연결 그래프의 부분 그래프 중 신장 트리는 여러 개일 수 있습니다.
최소 비용 신장 트리 MST, Minimum Spanning Tree란?
트리를 구성하는 간선들의 가중치 합이 최소인 신장 트리를 말합니다.
프림 Prim과 크루스칼 Kruskal 알고리즘을 통해 MST를 찾을 수 있습니다.
- MST의 활용
- 도로 건설: 도시들을 모두 연결하면서 도로의 길이가 최소가 되도록 하는 방법
- 전기 회로: 단자들을 모두 연결하면서 전선의 길이가 가장 최소가 되도록 하는 방법
- 통신: 전화선의 길이가 최소가 되도록 하면서 전화 케이블 망을 구성하는 방법
- 배관: 파이프를 모두 연결하면서 파이프의 총 길이가 최소가 되도록 연결하는 방법
- 크루스칼 알고리즘 Kruskal Algorithm
가중치를 기준으로 간선을 정렬하고 MST가 될 때까지 간선을 하나씩 선택 또는 삭제해 나가는 방법입니다.
가중치가 가장 적은 간선을 선택해 나가기 때문에 그리디 알고리즘을 기반으로 합니다.
크루스칼 알고리즘의 시간복잡도는 O(E log E)입니다.
- 구현 과정
- 간선 없이 정점들만으로 그래프를 초기화합니다.
- 가중치를 기준으로 간선을 오름차순 정렬합니다. -> O(E log E)의 시간복잡도가 소요됩니다.
- 가중치가 가장 작은 간선부터 Cycle이 생기지 않으면 추가하고, Cycle이 생기면 추가하지 않습니다.
- 모든 정점을 포함하는 MST가 완성될 때까지 3의 과정을 반복합니다.
* 참고 https://8iggy.tistory.com/160
크루스칼 알고리즘(Kruskal's Algorithm)
읽기 전 불필요한 코드나 잘못 작성된 내용에 대한 지적은 언제나 환영합니다. 개인적으로 사용해보면서 배운 점을 정리한 글입니다. 크루스칼 알고리즘이란? 최소 신장 트리(Minimum Spanning Tree)
8iggy.tistory.com
- Cycle 판단하기
Cycle을 판단하는 방법은 합집합 찾기 Union-Find 기법을 활용할 수 있습니다.
서로소 집합 Disjoint-Set 알고리즘이라고도 불리며, 두 노드가 같은 그래프에 속하는지를 판별합니다.
두 노드의 루트 노드가 서로 다르면 다른 그래프이므로, 두 노드를 연결하여도 사이클이 존재하지 않는다는 것을 알 수 있습니다.
1. 초기화: 각 노드의 루트 노드를 자기 자신으로 초기화합니다.
2. Union 연산: 한 쪽 노드의 루트 노드를 다른 한 쪽의 루트 노드로 바꿔 두 노드가 속한 트리를 합칩니다. -> O(1)의 시간복잡도가 소요됩니다.
3. Find 연산: 두 노드의 루트 노드를 비교하여 같은 트리에 속하는지 확인합니다. -> O(h)의 시간복잡도가 소요됩니다.
* 참고 https://8iggy.tistory.com/157
서로소 집합(Disjoint Set), 유니온 파인드(Union-Find)
읽기 전 불필요한 코드나 잘못 작성된 내용에 대한 지적은 언제나 환영합니다. 개인적으로 배운 점을 정리한 글입니다. 유니온 파인드란 서로소 집합(Disjoint Set)을 표현할 때 사용하는 알고리즘
8iggy.tistory.com
- 프림 알고리즘 Prim Algorithm
한 개의 정점으로 이루어진 그래프로 초기화 한 후, 그래프에 속한 정점과 다른 정점을 연결하는 간선 중 가장 작은 가중치인 간선을 선택해 MST를 구성해 나가는 방법입니다.
프림 알고리즘 또한 매 순간 최선의 선택을 해나가는 그리디 알고리즘 기반입니다.
프림 알고리즘의 시간복잡도는 O(E log V)가 소요됩니다.
- 구현 과정
- 임의의 한 정점만을 포함하는 그래프로 초기화합니다.
- 그래프에 속한 정점들과 인접한 정점들 중 Cycle을 형성하지 않으면서 가장 작은 가중치의 간선과 연결된 정점을 그래프에 추가합니다.
- 모든 정점을 포함하는 MST가 완성될 때 까지 2의 과정을 반복합니다.
* 참고 https://8iggy.tistory.com/159
프림 알고리즘(Prim's Algorithm)
읽기 전 불필요한 코드나 잘못 작성된 내용에 대한 지적은 언제나 환영합니다. 개인적으로 사용해보면서 배운 점을 정리한 글입니다. 프림 알고리즘(Prim's Algorithm)이란? 최소 신장 트리(Minimum Span
8iggy.tistory.com
출처
Graphs in Data Structure: Overview, Types and More [Updated] | Simplilearn
Explore what are graphs in data structure, its types, terminologies, representation and operations. Read on to know how to implement code in graph data structure. Keep learning!
www.simplilearn.com
Graphs in Computer Science
Disconnected Graphs Vertices in a graph do not need to be connected to other vertices. It is legal for a graph to have disconnected components, and even lone vertices without a single connection. Vertices (like 5,7,and 8) with only in-arrows are called sin
web.cecs.pdx.edu
Difference Between Directed and Undirected Graph | Compare the Difference Between Similar Terms
Directed vs Undirected Graph A graph is a mathematical structure that is made up of set of vertices and edges. A graph represents a set of objects (represe
www.differencebetween.com
Data Structure & Algorithms - Spanning Tree
Data Structure & Algorithms - Spanning Tree A spanning tree is a subset of Graph G, which has all the vertices covered with minimum possible number of edges. Hence, a spanning tree does not have cycles and it cannot be disconnected.. By this definition, we
www.tutorialspoint.com
'Computer Science > Data Structures' 카테고리의 다른 글
| 맵 Map과 해시 Hash (2) | 2022.05.18 |
|---|---|
| [비선형 구조] 트리 Tree (0) | 2022.05.15 |
| [선형 구조] 스택과 큐 (0) | 2022.05.14 |
| [선형 구조] 리스트 (0) | 2021.07.18 |
| Prologue. 자료구조 (0) | 2021.06.28 |